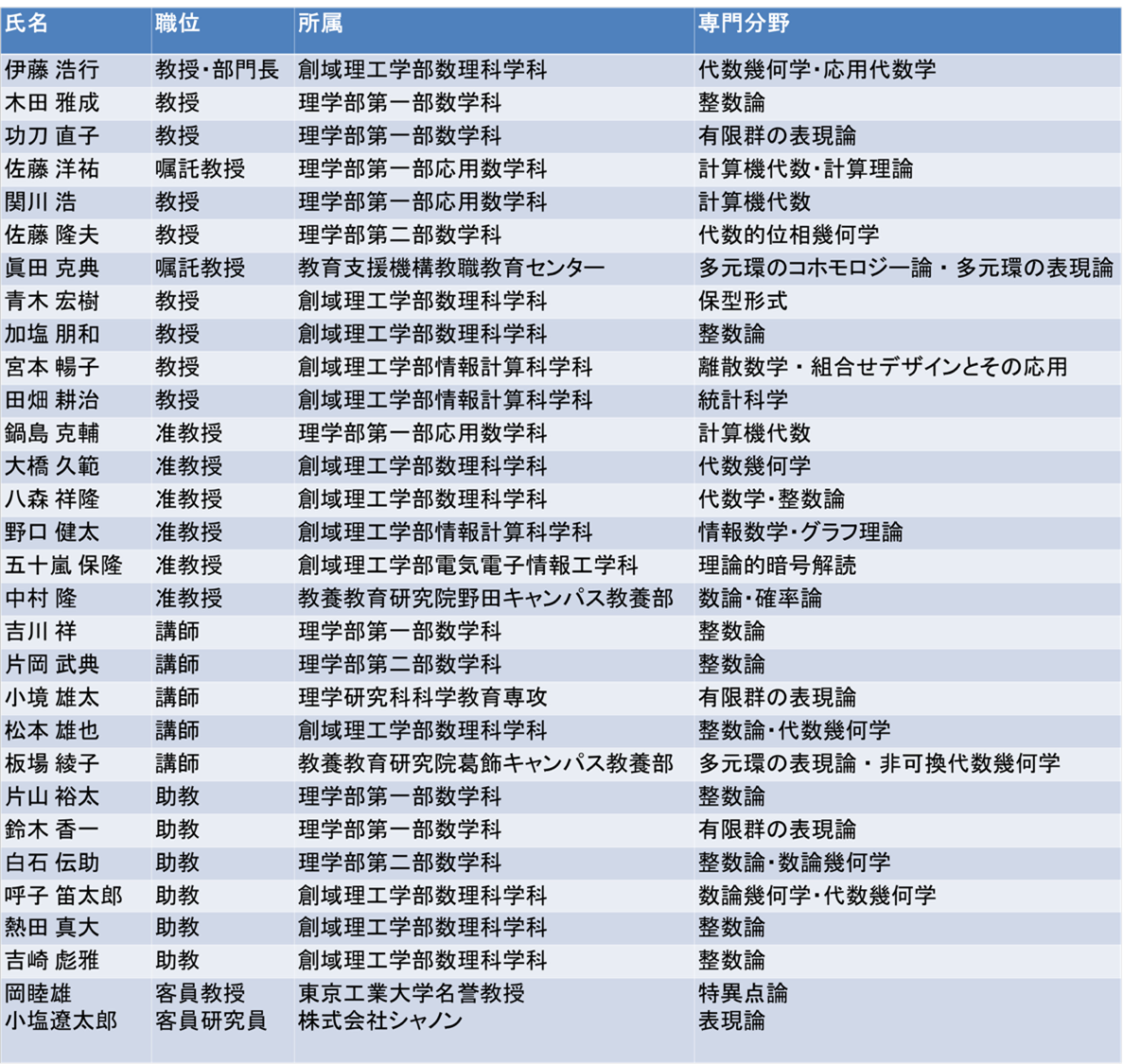
現代代数学諸分野の理論研究、および応用諸分野との融合研究

「先端的代数学融合研究」研究部門設立の背景と目的

学問として2000年以上の歴史を持つ数学にとって、異分野との相互作用は学問の深化のために非常に重要なファクターのひとつです。純粋数学は代数学、幾何学、解析学に大きく分類されますが、代数学と解析学は幾何学（的対象）を軸として車輪の両輪と捉えることが出来ます。その長い歴史の中で、多くの理工学諸分野が連続的対象を主に扱う解析学と影響を及ぼし合ってきましたが、20 世紀以降、情報科学や情報工学、電気電子工学や機械工学などにおいて、離散的対象を主に扱う代数学との連携が行われ、新しい研究を生み出しています。代数学をベースとした広がりを持つ本部門は、解析学を中心とした「数学解析連携研究部門」と緩やかな連携を結びながら、代数学を中心に理工学全体を支える基礎科学としての数学の発展に寄与し、その上にたつ連携分野との融合研究を行い、東京理科大ならではの研究拠点として未来に貢献する研究を推進することを目標とするものです。

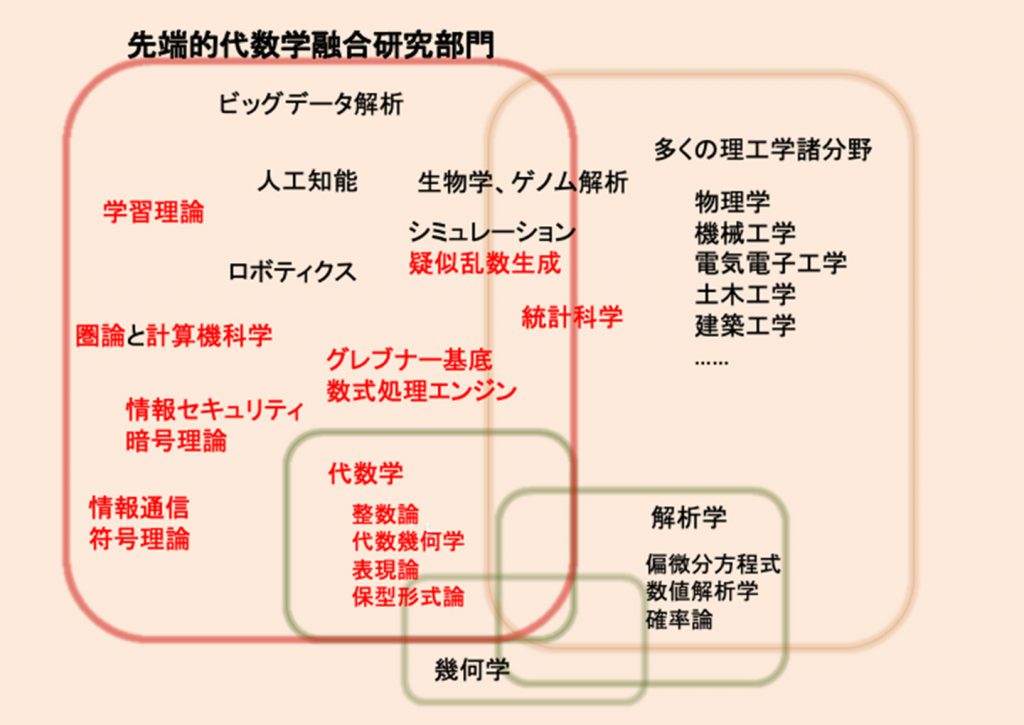
「先端的代数学融合研究」部門における研究内容

本研究部門は、学内に分散する整数論、数論幾何学、代数幾何学、可換環論、表現論、保型形式論、代数的位相幾何学などの代数学中心の研究者に加え、離散数学、組合せデザイン、計算機代数学、計算論理学、暗号理論、符号理論、応用代数学、統計科学などの代数学ベースの応用研究を扱う研究者から構成されております。これまで、分野の垣根や大学の枠を越えた、セミナーやワークショップ、国際会議などの開催を通じて緩やかな連携関係を保ってきました。今後も、この関係を強化し、これまで個人レベルで行われてきた部門内や学外研究者、さらには民間企業研究者との間の共同研究を、個対多の関係へ進展させ、部門から多くの基礎研究および連携・融合研究を生み出し発展させます。

具体的に部門内に設置される研究グループは、基礎研究3 グループ、応用研究4 グループがあり、グループ相互に連携をとり合いながら研究を行います。

基礎グループは代数幾何学講演会、整数論講演会、神楽坂代数学セミナー、特異点・トポロジーセミナー、野田代数幾何学ワークショップを定期的に開催し、連携をとりながら研究を推進します。一方、応用グループは基礎グループと連携を図り、共同セミナーや特定分野の学内外講師による応用数理講演会などにより、異分野間の連携の要となる「出会いの場」や「議論の場」を積極的に提供し、研究活動の起爆剤とします。また、2020年1月に調印された、本学研究推進機構総合研究院と東北大学数理科学連携研究センターとの協定に基づき、数理解析連携研究部門との協働により共同研究や研究集会の共同開催を定期的に行い、研究を大きく発展させていきます。

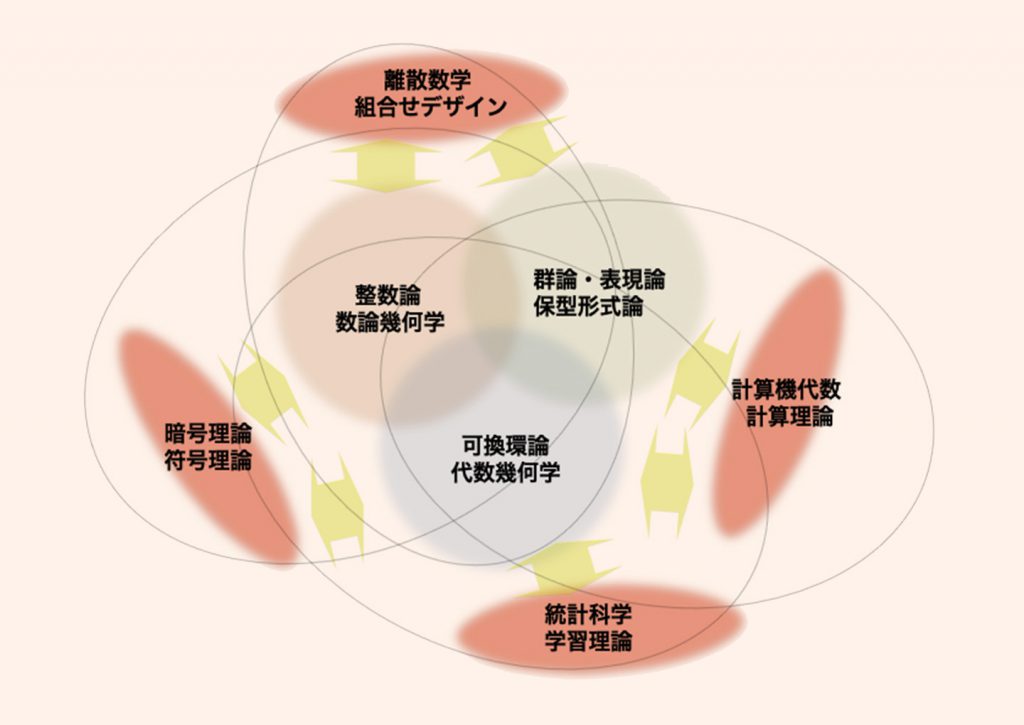
本部門は基礎グループ、応用グループいずれも理論中心の部門であり、

1）学内の多くの学科(8学科)に分散している幅広い層の研究者の連携であること、2）国内外での共同研究実績が豊富であること（欧州4カ国、アジア2カ国、国内研究機関18カ所、民間3企業）、3）セミナーやシンポジウムの定期開催による連携が継続的に行われてきたこと、などが特色として挙げられます。

将来展望

当部門の前身である「現代代数学と異分野連携研究部門」においては、多くの基礎研究が進展し相互連携が図られるとともに、国内外から多くの研究者の参加による定期的セミナー・研究集会が開催され代数学研究拠点としての役割を果たしてきた。東北大学数理科学連携研究センターとの連携も少しづつ動きだし、セミナー・研究集会の共同開催や共同研究へ発展している。数理解析連携研究部門と当部門が受け皿であるので両部門で協働し、今後は人的交流も含めて連携を大きく発展させていきたいと考えております。

代数学ベースの異分野連携は20世紀後半から急速に重要性を増し、21世紀になった今日も思いがけない新たな連携分野が発見されています。「数理科学連携研究部門」と共同で行う技術相談窓口を通じて、また関連する部門である「デジタルトランスフォーメーション研究部門」との連携により、今後、新たな代数学ベースの異分野連携・融合研究を開拓していきます。