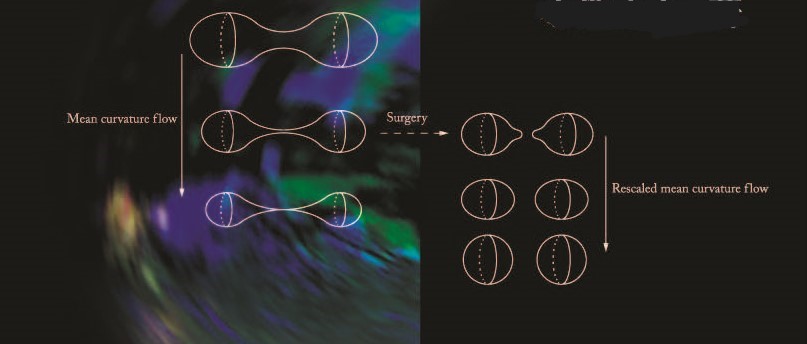
幾何学は、微分幾何学、位相幾何学(=トポロジー)、及び代数幾何学の3つの分野に分けられます。微分幾何学は、元々は、ある幾何構造gを備えた多様体M(連続性と微分可能性を扱える空間)内の図形の性質で、gを不変に保つMの変換達によって不変なものを調べる学問(リーマン幾何学、ローレンツ幾何学,シンプレクティック幾何学等)でした。ここで、gを不変に保つMの変換の全体は、リー群(適切な群構造備えた多様体)になることを注意しておきます。その後、物理学におけるゲージ理論の発展と共に、(M,g)上の主バンドルやそれに同伴するベクトルバンドルの接続理論へと発展しました。例えば、重力場と電磁場を統一した相対論的理論は、4次元ローレンツ多様体(ローレンツ計量gを備えた4次元多様体)とよばれる空間上の1次ユニタリ群U(1)を構造群にもつ主バンドル、及びその随伴ベクトルバンドルの接続理論を用いて、研究されます。このように、微分幾何学は、リー群作用の理論やゲージ理論等と密接な関わりをもち、それゆえ、量子力学や物性学へ応用されます。また、体積汎関数やエネルギー汎関数の(-1)倍の勾配流である平均曲率流や調和流を研究する幾何解析学(これは微分幾何学と解析学を用いて研究する学問)は、粒界をはじめとする界面の研究や結晶構造等の物性学の研究と密接な関わりをもちます。この研究は、分子生物学における環状のDNA・RNAの微妙な形状(これらの螺旋構造の微妙な曲がり具合)の研究にも役に立ちます。さらに、粒界の強度の研究の複合材料力学への応用が考えられます。
一方、位相幾何学は、位相空間とよばれる連続性のみを扱える空間、及びその空間内の図形の性質で連続的な変形に関して不変なものを調べる柔らかい幾何学であり、その研究には、ホモトピー群やホモロジー群とよばれる代数的な位相不変量も用いられます。その一分野として、結び目理論があります。結び目理論とは、3次元ユークリッド空間や3次元球面等の3次元位相多様体(局所ユークリッド的な位相空間)X内に連続的に埋め込まれた2つの円(正確には円周)がXの同相写像(Xからそれ自身への連続性を保つ1対1対応のこと)で写り合うことができるかどうか等を調べる理論です。この理論は、分子生物学におけるDNA・RNA(閉じた螺旋構造をもつもの)の大域的な研究と密接な関わりをもち、これらの研究を数学的に行うために重要な理論として位置づけられています。結び目理論、さらに写像類群論は、ゲージ理論を用いても研究され(このような研究は,位相的場の理論とよばれます)、ゲージ理論とも密接な関わりをもちます。また、代数幾何学は、アフィン空間や射影空間上のいくつかの多項式の共通零点集合のなす図形の性質を調べる幾何学であり、この研究は、主バンドルのある種の接続全体のなす空間のモジュライ空間の研究等に用いられ、それゆえ、主バンドルの接続理論を用いて数学的に研究されるゲージ理論の研究と密接な関わりをもちます。
以上のように、幾何学の各分野は、量子力学,物性学,分子生物学,及び,粒界・複合材料力学等の自然科学の研究と密接な関わりをもちます。
本研究部門では、量子力学、物性論、分子生物学、及び粒界・複合材料力学等の自然科学の包括的な幾何学的理論を構築し、自然科学の各分野へフィードバックすることを目指します。具体的に、以下の4つの研究を行います。
I 幾何解析学の視点からの物性の研究
II 幾何的ゲージ理論の視点からの量子ウォークの研究
III 結び目理論・場の量子論・幾何学的変分学を用いたDNA・RNAの研究
IV 幾何解析学の視点からの粒界の研究,及び複合材料力学への応用
これら4つの研究方法の詳細については、本研究部門のオリジナルホームページの 部門概要のページをご覧ください。
RIST-TUS-Geo.Nat.Sci.-about-j