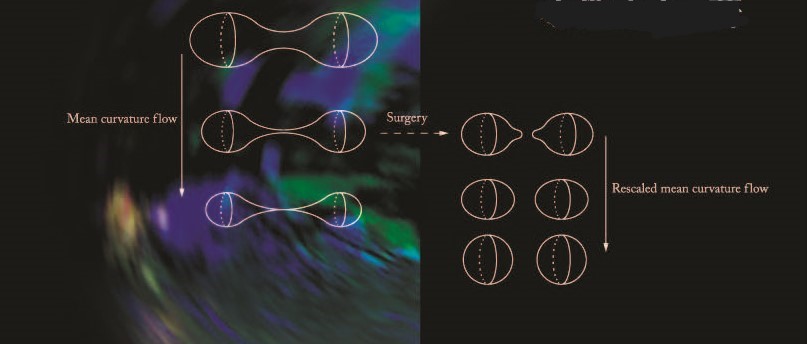
In this research division, we aim to construct the comprehensive geometric theory for the quantum mechanics, the condensed matter physics, molecular biology and grain boundary-composite materials mechanics, and feedback it to the above four fields. The geometry is divided broadly into three fields of the differential geometry, the topology and the algebraic geometry. In the differential geometry, it was originally aimed to research a differential manifold M equipped with a geometric structure g (where a differentiable manifold means the space where the continuity and the differentiability of maps between the spaces can be defined) and investigate the properties of figures in the space (M,g) which are invariant under transformations of M preserving g invariantly. Note that the whole of such transformations of M preseriving g invariantly is a Lie group (that is, a differentiable manifold equipped with a suitable group structure). Later, in the differential geometry, it also has been aimed to research the theory of the connections of principal bundles and vector bundles over the space (M,g) in order to research the gauge theory (in the thoretical physics) from the viewpoint of the differential geometry. For example, the theory unifying the gravitational field and the electromagnetic field is researched on the principal bundle having the unitary group U(1) of degree one as the structure group over a 4-dimensional Lorentzian manifold (M,g). Thus the differential geometry is closely connected to the theory of Lie group actions and the gauge theory, and hence can be applied to the researches of the quantum mechanics and the condensed materials physics. In the geometric analysis (which is researched by using both of the differential geometry and the analysis), the mean curvature flow and the harmonic flow etc. are researched, where the mean curvature flow means the gradient flow of the (-1)-multiple of the volume functional, and the harmonic flow means the gradient flow the (-1)-multiple of the (usual) Energy functional). We aim to apply these researches to those of the grain boundary and the cluster. Also, we aim to apply these researches to that of the shape of double helices of polydeoxyribonucleotides constructing DNA etc. in the molecular biology. Furthermore, we aim to apply the research of the strength of the grain boundary to that of the composite materials mechanics.
The topology aims to research a toplogical space X (where can be defined the continuity of maps between the spaces) and investigate the properties of the figures in X which are invariant under continuous transformations of X. Also, the various algebraic topological invariants (for example, the homotopy group and the homology group) are used in this research. The knot theory is very important in the research field of the topolgy and the research of DNA・RNA. The kont means a circle S^1 continuously embedded into the 3-dimensional sphere S^3 (or the 3-dimensional Euclidean space R^3). Here we note that knots in R^3 are regarded as knots in S^3 because R^3 is identified with an open portion of S^3. Main research thema of the knot theory is to investigate whether two knots in S^3 are mapped to each other by a homeomorphism of S^3 (=a continuous one-to-one map of S^3 onto oneself such that its inverse also is continuous). The knot theory is important in the research of the topoloogical global structure (the structure of double helices) of polydeoxyribonucleotides constructing circular DNA (in the molecular biology). Also, knots and the mapping class group are sometimes researched by using the gauge theory, which is one of so-called the topological field theory.
In the algebraic geometry, are researched the structure of the common zero-point set of some polynomials over the affine space or the projective space. This research is used to investigate the moduli space of the space of various kind of connections of the principal bundle and hence is applied it to various reseaches of the gauge thoery. As above, each research field of the geometry are connected closely to those of the quantum mechanics, the condensed matter physics, molecular biology and grain boundary-composite materials mechanics. In detail, we aim to perform the following four researches.
I The research of the condensed matter physics in the view-point of the geometric variational theory
II The research of the quantum walk in the view-point of the geometric gauge theory
III The research of DNA・RNA in the view-point of the knot theory, the topological field theory and the geometric variational theory
IV The research of the grain boundary in the view-point of the geometric analysis and its application to the composite materials mechanics
About the detail of the research methods of the above I~IV, see the following page in the original homepages of this research division.